푸리에 변환과 라플라스 변환의 차이

 

 

---

 

안녕하세요.

푸리에 변환과 라플라스 변환은 신호나 시스템을 주파수 도메인에서 분석하기 위한 강력한 도구로, 공학과 물리학의 여러 분야에서 널리 사용됩니다. 두 변환은 모두 주파수 영역으로 신호를 변환해 다양한 분석을 가능하게 하지만, 그 특성과 용도에는 중요한 차이가 있습니다. 이 글에서는 푸리에 변환과 라플라스 변환의 기본 개념과 차이점, 그리고 각 변환이 쓰이는 실제 응용 분야에 대해 자세히 설명해 보겠습니다.

---

아래 푸리에 변환과 라플라스 변환에 대한 자세한 내용 참조해보세요

1. 푸리에 변환

https://semicircuit.tistory.com/entry/%ED%91%B8%EB%A6%AC%EC%97%90-%EB%B3%80%ED%99%98-Fourier-Transform-%ED%91%B8%EB%A6%AC%EC%95%A0-%ED%8A%B8%EB%9E%9C%EC%8A%A4%ED%8F%BC-%EC%8B%9C%EA%B0%84%EA%B3%BC-%EC%A3%BC%ED%8C%8C%EC%88%98-%EB%B3%80%ED%99%98

 

2. 라플라스 변환

https://semicircuit.tistory.com/entry/%EB%9D%BC%ED%94%8C%EB%9D%BC%EC%8A%A4-%EB%B3%80%ED%99%98-Laplace-Transform-%EB%B3%B5%EC%86%8C-%EC%A3%BC%ED%8C%8C%EC%88%98-%EB%B3%80

 

※1. 푸리에 변환과 라플라스 변환의 기본 개념 

▶1. 푸리에 변환 

푸리에 변환은 주기적이거나 안정된 신호를 실수 주파수 영역으로 변환하여, 주파수 성분들을 시간 함수에서 분리합니다. 푸리에 변환은 주파수 분석에 주로 사용되며, 신호의 주파수 분포와 진폭을 이해하는 데 유용합니다.

 

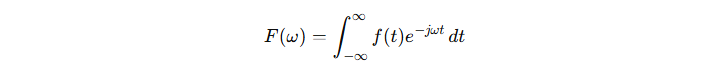
▶2. 라플라스 변환 

라플라스 변환은 시간 도메인 신호를 복소 주파수 영역으로 변환하여, 신호의 감쇠(또는 성장)와 주파수를 동시에 표현할 수 있습니다. 시스템의 초기 상태와 과도 응답을 포함한 전체 동작을 쉽게 분석할 수 있어 동적 시스템의 해석에 자주 사용됩니다.

 

 

 

 

※2. 푸리에 변환과 라플라스 변환의 주요 차이점

▶1. 변환 영역의 차이 

 

• 푸리에 변환은 실수 주파수(ω)를 사용하여 주파수 성분만을 분석합니다. 이는 신호가 감쇠하지 않거나 일정하게 유지되는 경우에 적합합니다.
• 라플라스 변환은 복소수 주파수 s=σ+jω 이용하며, 주파수 성분과 감쇠 성분을 동시에 다룹니다. 이로 인해 라플라스 변환은 비주기적이고 감쇠하는 신호를 다루는 데 더 유리합니다.

 

▶2. 시간 특성

 

• 푸리에 변환은 일반적으로 무한 시간 신호에 대해 정의됩니다. 이는 신호가 −∞부터 +∞까지 이어지는 안정적인 상태에 적합하며, 주기적 신호 분석에 유리합니다.
• 라플라스 변환은 대부분 t=0 이후의 신호를 다루며 초기 상태와 과도 상태를 포함한 신호 분석이 가능합니다. 시스템의 응답을 시간에 따라 감쇠 또는 증폭하는 효과를 분석할 수 있어, 비주기적 신호에 유리합니다.

 

▶3. 초기 조건 반영

 

• 푸리에 변환은 신호의 초기 조건을 반영하지 않으며, 주로 주파수 성분만을 분석합니다. 초기 조건이 중요한 시스템이나 회로 해석에는 제한적입니다.
• 라플라스 변환은 시간 도메인에서의 초기 조건을 반영할 수 있어, 초기 값 문제와 과도 상태 분석이 필요할 때 효과적입니다. 제어 시스템이나 회로 설계에서 중요한 역할을 합니다.

 

▶4. 수렴 조건

 

• 푸리에 변환은 신호의 에너지가 유한해야 합니다. 즉, 푸리에 변환은 제곱 적분 가능한 신호에만 적용될 수 있어, 감쇠하지 않는 신호나 발산 신호에는 사용이 어렵습니다.
• 라플라스 변환은 신호에 감쇠 성분이 포함될 수 있어 발산 신호에도 적용 가능합니다. 이는 라플라스 변환이 다양한 신호와 시스템에 대해 더 광범위한 수렴 조건을 갖게 합니다.

 

 

 

※3. 푸리에 변환과 라플라스 변환의 관계

라플라스 변환을 특정한 경우로 단순화하면 푸리에 변환을 얻을 수 있습니다. 라플라스 변환에서 감쇠 성분(σ)을 0으로 설정하고, s=jω로 두면 푸리에 변환이 됩니다. 즉, 푸리에 변환은 라플라스 변환의 특수한 형태라고 할 수 있으며, 푸리에 변환이 안정적 신호 분석에 주로 사용되는 이유도 이 관계에서 설명됩니다. 

 

 

 

※4. 푸리에 변환과 라플라스 변환의 응용 차이

▶1. 푸에 변환의 응용 

 

• 음향 및 영상 처리: 신호를 주파수 성분으로 분석해 특정 주파수를 필터링하거나 변형하는 데 활용됩니다.
• 통신 시스템: 주파수 대역 분석 및 신호 변조에 필수적이며, 디지털 신호 처리(DSP)에도 폭넓게 사용됩니다.
• 진동 및 구조 분석: 구조물의 진동 모드를 분석하여 내진 설계 등에 응용됩니다.

 

 

▶2. 라플라스 변환의 응용 

 

• 제어 시스템 설계: 시스템의 안정성 분석, 제어기 설계, 과도 응답 분석 등에서 핵심적으로 사용됩니다. 시스템의 전달 함수(Transfer Function)로 안정성과 응답 특성을 분석할 수 있습니다.
• 회로 해석: RLC 회로의 초기 상태와 과도 상태를 포함한 회로 해석에 유리하여, 충전 및 방전 과정을 쉽게 계산할 수 있습니다.
• 기계 시스템: 스프링-댐퍼와 같은 시스템의 과도 상태와 감쇠 해석에 자주 사용됩니다.

 

 

 

 

 

※5. 요약: 푸리에 변환과 라플라스 변환의 차이

구분푸리에 변환라플라스 변환

	푸리에 변환	라플라스 변환
시간 특성	주기적, 안정적 신호 분석에 적합	비주기적, 감쇠 신호 및 과도 상태 분석에 적합
초기 조건 반영	초기 조건 반영이 어려움	초기 조건 반영이 용이
수렴 조건	에너지가 유한한 신호에 적용 가능	발산 신호도 포함 가능, 수렴 조건이 넓음
주요 응용	주파수 분석 (음향, 영상 처리, 통신 등)	시스템 해석, 안정성 분석, 제어 및 회로 해석
변환 영역	실수 주파수 영역 (ω\omegaω)	복소 주파수 영역 (s=σ+jωs = \sigma + j\omegas=σ+jω)

 

 

 

 

푸리에 변환과 라플라스 변환은 신호 및 시스템 해석에 있어 각각의 강점이 있으며, 분석 대상의 특성에 맞춰 적절하게 선택됩니다. 푸리에 변환은 주파수 성분 분석에 특화되어 주기적 신호와 안정적인 시스템에서 유리하며, 라플라스 변환은 초기 조건과 과도 응답을 고려해 비주기적 신호와 동적 시스템을 분석하는 데 뛰어납니다. 

 

이상으로 푸리에 트랜스 변환과 라플라스 변화의 차이에 대한 설명을 마치겠습니다. 감사합니다.