안녕하세요.
지난 포스트에서 비동기 카운터에 대해 기술하였습니다. 이번 포스트에서는 동기 카운터에 대해 기술하겠습니다.
순서논리 회로에는 다양한 내용이 있습니다. 필요에 따라 아래 글들도 참고해보세요~!!~
1. Latch(래치)와 Flip-flop(플립플롭)
https://semicircuit.tistory.com/37
2. 비동기 카운터
https://semicircuit.tistory.com/38
3. 동기 카운터
https://semicircuit.tistory.com/39
4. 불규칙 카운터
https://semicircuit.tistory.com/40
5. State Machine 설계
https://semicircuit.tistory.com/41
6. UP/DOWN Counter
https://semicircuit.tistory.com/42
7. 시프트 레지스터
https://semicircuit.tistory.com/43
※1. 카운터의 정의
▶1. 종류
⓵ (클럭의 사용에 따른) : 비동기 카운터( 처음 J-K 플립플롭만 Clock신호를 받음) / 동기 카운터 모든( J-K플립플롭에 Clock신호를 받음)
⓶ (수의 변화에 따른) : Up카운터(0,1,2,3...) / Down카운터(내림차순 ....3,2,1,0)
⓷ (허용 범위(모듈러스)에 따른) : 4진(0~3), 8진(0~7), 10진(0~9), etc...
▶2. 사용
: 수를 세는데 사용되는 하드웨어 디지털 회로, 클럭 펄스가 하나씩 인가될 때마다 미리 정해진 순서대로 상태가 반복되는 순차회로이다.
=> 입력되는 클럭의 수를 센다.
▶3. 특징
: 7-Segment를 통하여 다이오드에 표시되는 숫자로 변환하여 인간이 알아볼 수 있는 정보로 변환이 가능하다.
높은 주파수를 낮은 주파수로 바꿔주는 기능을 하여 ‘분주기’라고도 한다. => n단의 카운터회로는 클럭주파수를 1/2n의 신호로 반환 한다.
=> ex) clock의 주파수가 16MHz일 때, Q0는 8MHz, Q1은 4MHz Q2는 2MHz의 주파수를 가지고 있다.
▶4. 사용 소자와 개
:ex) N진 카운터
⓵ 나타내는 숫자 N개, 범위(모듈러스)가 0~(N-1)
⓶ 비트수 : 2^(n-1)<N<=2^n에서 => 비트수 n개 => n비트 카운터
⓷ J-K플립플롭의 개수 : n개
⓸ 출력 개수 = F/F개수

※2. 동기 카운터
- 카운터 내부에 있는 모든 플립플롭이 공통의 클록 펄스에 의해서 동시에 상태가 변하는 카운터이다.(동기 카운터 특징)
- 일단 모든 F/F의 C에 CLK를 연결하고 시작
- FF0의 JK는 HIHG(1)에 연결 이외의 FF의 JK는 앞단의 Q와 연결한다.
- 3비트 카운터 부터는 AND게이트를 통해 앞단과 그 앞단의 Q를 AND로 JK에 넣어 주면 delay가 줄어든다. 최대 (F/F의 개수 - 2)개 사용 가능
ex) J2와 K2의 입력에 Q1과 Q2를 AND로 받은 출력을 넣어준다.
ex) 4진 카운터



▶1. 동기 카운터의 전파지연(propagation delay)
- CLK의 신호가 각각의 C에 동시에 입력되면서 발생하는 delay(glitch)를 제외하고는 발생하지 않는다. => 매우 적은 propagation delay
3) Clear 단자를 이용하여 2^(n-1)<N<2^n 진 카운터 만들기
ex) 동기식 10진 카운터 만들기 (비동기식과 동일)
- 2^(n-1)<N<2^n의 경우 2^n의 카운터에서 일부 절단 시퀀스(truncated sequence)를 한다. ex) 10진 카운터는 1010에서 clear(절단,리셋)시킨다.
- Q0 Q1 Q2 Q2에서 Q0이 LSB, Q3가 MSB이다.
- 리셋 되어야 하는 부분에서 HIGH가 되는 FF의 Q를 NAND의 입력에 연결하고 NAND의 출력부는 모든 F/F의 Clear단자와 연결한다.
(2진수로 바꿨을 때 1의 개수 = NAND의 입력 개수)
이처럼 부분적 decoding(Q1' Q2')을 : partial 디코딩이라고한다. <=> Full 디코딩

cf)Full decoding 방법
NAND의 출력부는 동일하고 입력부에 0되는 F/F의 반전 출력도 같이 입력한다.
=> 이렇게 하는 것이 partial 디코딩에 비해 안정적

※3. Design of Counters with Excitataion table(여기표를 이용한 동기 카운터 설계)
▶1. 동기 카운터의 설계 과정
⓵ 상태도 : 출력을 순환하는 방식으로 표현하는 것
⓶ 다음 상태표 작성 : 현재와 다음 상태를 표현하는 것
⓷ 플립플롭 전이표 작성 : 다음 변화에 대한 J-K의 입력을 나타내는 표를 작성하는 것
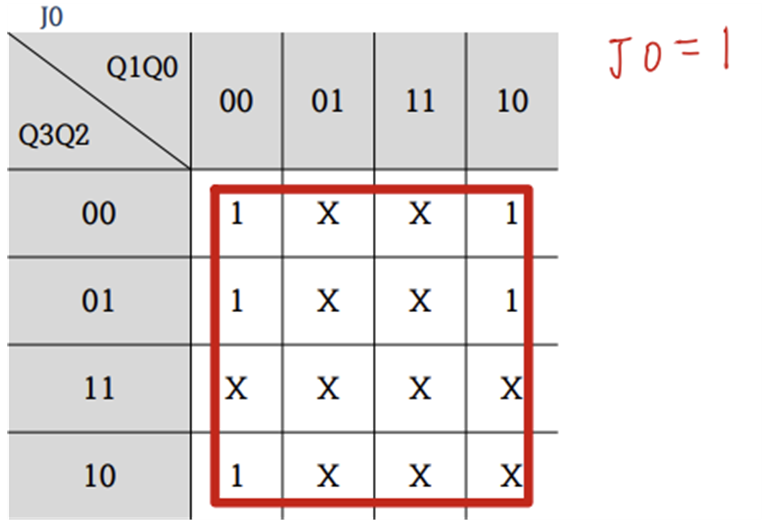
⓸ 카르노맵 작성 : Present State와 Excitation Table을 카르노맵으로 표기하는 것
⓹ 플립플롭 입력에 논리식 : 카르노맵을 통해 수식으로 표현하는 것
⑥ 카운터 구현 : 수식으로 얻은 식을 회로로 설계하는 것
ex1) 10진 카운터의 동기 카운터 설계 - JK F/F
⓵ 상태도

⓶ 다음 상태표 작성

⓷ 플립플롭 전이표 작성

=> 전이표에 따라서 ( present State와 Next State를 비교 한후 전이표를 통한 값을 J-K의 해당 자리에 배치한다.)

=> 나머지(구현되지 않는 것들)은 don't care(x)로 처리한다.
⓸ 카르노맵 작성


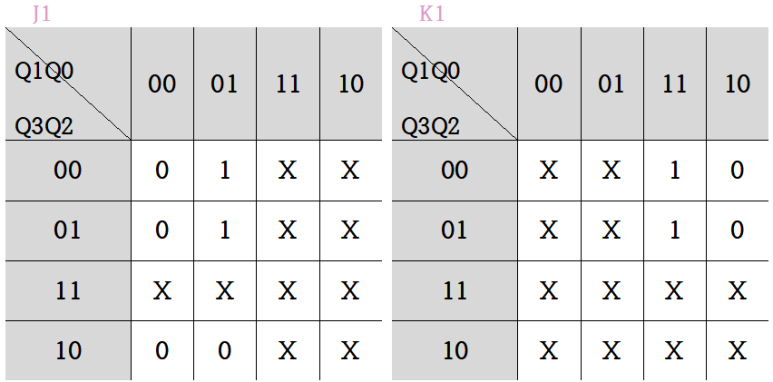

⓹ 플립플롭 입력에 논리식







⑥ 카운터 구현

으로 회로 설계
( F/F의클록 입력은 모두 CLK에 넣는 것은 전재로 한다.)
<기본구성요소>
1) 기본 구성 파악
- 20진 카운터 2^3<10<=2^4 이므로 4비트 카운터 사용
- 4비트 카운터 => 4개 J-K F/F 사용
- 출력부 개수 = F/F개수 => 6개
- 논리식을 봤을 때 AND게이트 4개 필요(J2,K2는 같은 출력이므로 합하여 1개만 사용),
NOT게이트 1개 사용(Q3)
- 플립플로1 4개 사용 => 출력 4개
<회로설계>

## 결과 ##
=> Clear를 사용하는 방법은 9.9999...처럼 10이 다되기 바로 직전 Reset하여 노이즈가 발생한다. 클럭 스피드가 아주 빠르면 문제가 발생 할 수 있다.
=> 앞선 과정(excitation table을 통한 설계)에서 JK F/F를 구성하는 10진 카운터를 설계 하였다.
결론을 먼저 말하면 이전 7장에서 학습한 Clear단자를 이용한 직관적 방법(암기성 방법)을 통한 카운터 설계는 토글 기능을 포함하고 있는 JK F/F와 T F/F에만 국한되어 있다. 하지만 앞선 과정을 통해 설계를 하면 우리가 배운 모든 F/F(SR, JK, T, D)에서 카운터 설계가 가능하다.
=> 모든 과정은 동일하나 각각에 F/F 특성에 따른 전이표의 차이로 회로가 차이가 난다.
cf) 일반적으로 토글 기능을 포함하는 JK F/F와 T F/F이 SR F/F와 D F/F에 비해 회로가 더 간단한 형태를 띈다.
ex2) 10진 카운터의 동기 카운터 설계 중 - SR F/F









=> 다음의 예제 2~4를 통해 같은 입력과 출력을 가진 조건의 카운터일지라도 플립플롭의 차이에 따라 전이표가 달라 플립플롭 입력이 달라지는 것을 볼수 있다. 이후 과정을 생략 하였지만 이를 통해 카르토맵을 통한 간략화 또한 JK F/F과는 각각 다른 결과를 나올 것이라는 것을 예상 할 수 있고, 그렇지만 같은 결과를 나타내는 것을 볼수 있다.
그러면 어떤 플립플롭을 사용하는 것이 가장 적합 할까??
다음의 6진 카운터의 4가지 플립플롭의 회로를 비교해 보면

1) JK F/F, T F/F VS SR F/F, D F/F
JK F/F와 T F/F의 경우 SR F/F과 D F/F보다 한눈에 보다오 더 적은 게이트를 사용하고 비교적 간단한 형태의 회로를 가지는 것을 볼 수 있다.
=> 일반적으로 JK F/F와 T F/F을 통한 회로 구성이 SR F/F와 D F/F으로 구성한 회로 설계보다 더 간단한 형태를 띈다.(토글의 유무 때문)
2) JK F/F VS T F/F
위의 경우에는 JK F/F이 T F/F보다 1개 더 적은 게이트를 사용하여 비교적 더 간단한 형태를 띄었지만 경우에 따라 T F/F이 더 간단할 때도 있다. 즉, 이 두 F/F은 경우에 따라 조금의 차이는 나지만 비슷하다고 보는 것이 좋다.
cf) excitation table을 작성할 때 작업이 많아 실수할 수도 있고 시간이 걸릴 수도 있는데 이때 공통 특성을 이용하면 비교적 편리하고 실수를 줄일 수 있다.
ex) 하나의 열씩 순서대로 채워 간다 했을 때,
SR F/F에서 S의 테이블을 채울 때 Q(t+1)=0이면 S는 무조건 0이다.
Q(t+1)=0인 부분의 S를 모두 0으로 먼저 채우고 나머지는 비교해서 채운다.

'University curriculum > [Course] Digital Engineering' 카테고리의 다른 글
| [디지털 공학(23)] State Machine(상태기계)_순서논리회로(5) (0) | 2024.05.11 |
|---|---|
| [디지털 공학(22)] 불규칙 카운터_순서논리회로(4) (0) | 2024.05.11 |
| [디지털 공학(20)] Asynchronism Counter(비동기 카운터)_순서논리회로(2) (0) | 2024.05.11 |
| [디지털 공학(19)] Latch(래치)와 Flip-flop(플립플롭)_순서논리회로(1) (0) | 2024.05.11 |
| [디지털 공학(18)] 패리티 발생기/검사기(Paity Detector) _조합논리회로(6) (0) | 2024.05.10 |



