![[디지털 공학(9)] 부울 대수와 논리 간략화](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FNqlhr%2FbtsHd9N6PWF%2FczmKpK9UYIXpA5wqx47G5k%2Fimg.png)

안녕하세요.
이번 시간에는 부울연산, 부울 계수, 드 모르간 법칙에 대해 알아보겠습니다.
※1. 부울 대수
▶1. Bool의 의의, 목적, 구성
-의의 : 1(참) 또는 0(거짓)의 값에 대해 논리 동작을 상태로써 표현되고 처리한다.
-목적 : 논리회로를 설계하고 분석하기 위함이다.
-구성 : 변수(동작,조건,데이터를 나타내는데 사용하는 기호),보수(변수의 역을 의미하여 변수위에 바를 사용), 문자(변수나 변수의 보수)
▶2. 부울 연산
(1) 부울 덧셈
- A+B, A'+B, A+B', A'+B'로 표시하며 OR연산과 동일하다.
(2) 부울 곱셈
- AB, A'B, AB', (AB)"로 표현하며 AND연산과 동일하다.
▶3. 부울 대수의 법칙

▶4. 연산자의 우선순위
=> 괄호>NOT>AND>OR
※2. 부울 대수의 규칙

+) A + A'B = A + B, 드모르간 법칙에 의한 규칙 : (AB)' = A' + Y', (A+B)' = A'B'
※3. 드모르간의 법칙
- 논리곱을 논리합으로, 논리합을 논리곱으로 바꾸어 쓰일 수 있다.
- NOR나 NAND를 이용하여 회로를 단순화하는데 유용하게 사용된다.
▶1. 드모르간 제1법칙
➀ 논리식 : (AB)' = A' + Y' / (ABC)' = A' + B' + C'
➁ 해석 : 논리곱의 전체 부정은 각각 변수의 부정을 논리합 한 것과 같다.
➂ 기호(Symbol) :

▶2. 드모르간 제2법칙
➀ 논리식 : (A+B)' = A'B' / (A+B+C)' = A'B'C'
➁ 해석 : 논리합의 전체 부정은 각각 변수의 부정의 논리합과 같다.
➂ 기호(Symbol) :

※4. 부울식의 표준형
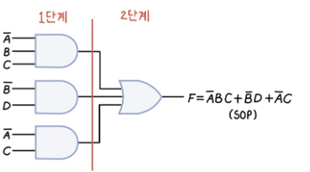
▶1. Minterm형식(Sum-of-product) : 곱셈 항들이 더해지는 형식
--> Minterm표준식 유도
- Minterm의 경우 출력(OUTPUT)이 1인 경우 입력 변수를 나열한다,
- 입력변수의 입력이 1인 경우 원래의 입력 변수, 0인 경우 보수로 대체하여 반환한다.
- 각각의 1의 출력에 대해 *(AND)를 한 이후 해당 논리들에서 +(OR)를 실행 한다.
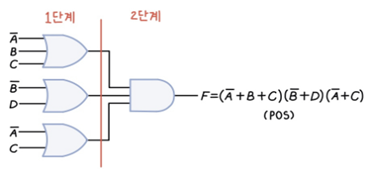
▶2. Maxterm형식(Product-of-sum) : 덧셈 항들이 곱해지는 형식
-->2 표준식 유도
- Maxterm의 경우 출력(OUTPUT)이 0인 경우 입력 변수를 나열한다,
- 입력변수의 입력이 0인 경우 원래의 입력 변수, 1인 경우 보수로 대체하여 반환한 다.
- 각각의 0의 출력에 대해 +(OR)를 한 이후 해당 논리들에서 *(AND)를 실행한다.
+) - SOP(Midterm)과 POS(Maxterm)은 서로 보수의 성질을 가진다.
- 두 회로는 간단한 회로설계를 가져올 수 있어 PLD로의 구현에 편리하다.
- Minterm와 Maxterm는 동일한 출력 결과를 가져 오는데 출력의 1과 0의 개수를 비교하여 1의 개수가 0의 개수보다 적으면 Minterm, 0의 개수가 1보다 적으면 Mindterm을 사용하여 회로를 간단하게 해준다.

'University curriculum > [Course] Digital Engineering' 카테고리의 다른 글
| [디지털 공학(11)] 논리회로의 해석(조합논리회로, 순서논리회로) (0) | 2024.05.09 |
|---|---|
| [디지털 공학(10)] 카르노맵 (0) | 2024.05.09 |
| [디지털 공학(8)] 고정 및 프로그래밍 가능 논리, 전파 지연 시간(Propagation Delay), 팬 아웃 (0) | 2024.05.08 |
| [디지털 공학(7)] 논리 게이트의 이해 (1) | 2024.05.08 |
| [디지털 공학(6)] 디지털 코드(BCD, Gray, ASCII, Parity) (0) | 2024.05.08 |

전자공학 블로그에 오신 것을 환영합니다! 최신 기술 동향, 회로 설계, 반도체 및 전자 부품에 대한 유용한 정보와 실습 팁을 제공합니다.
![[디지털 공학(11)] 논리회로의 해석(조합논리회로, 순서논리회로)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fqf5UK%2FbtsHdvYdnDm%2FUacqQSQ2Q8WbIL4X8jVms0%2Fimg.png)
![[디지털 공학(10)] 카르노맵](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FOAoIQ%2FbtsHbQvxeYU%2FHD8b1aV0WcT7lbeeH9enJk%2Fimg.png)
![[디지털 공학(8)] 고정 및 프로그래밍 가능 논리, 전파 지연 시간(Propagation Delay), 팬 아웃](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fbb6swO%2FbtsHcUDU9wC%2FaKkUfPkPSYIxRVBBMIlkKk%2Fimg.png)
![[디지털 공학(7)] 논리 게이트의 이해](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbkuT6K%2FbtsHbpZuCNY%2F8eQMthHVm9SLCOki3HOZf0%2Fimg.png)