![[디지털 공학(10)] 카르노맵](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FOAoIQ%2FbtsHbQvxeYU%2FHD8b1aV0WcT7lbeeH9enJk%2Fimg.png)

안녕하세요.
이번 시간에는 카르노맵에 대해 알아보겠습니다.
드모르간 법칙은 지난 포스트의 불연산이 필연적으로 선행되어야 합니다. 아래 링크 남겨두겠습니다.
https://semicircuit.tistory.com/27
[디지털 공학(9)] 부울 대수와 논리 간략화
안녕하세요.이번 시간에는 부울연산, 부울 계수, 드 모르간 법칙에 대해 알아보겠습니다. ※1. 부울 대수 ▶1. Bool의 의의, 목적, 구성-의의 : 1(참) 또는 0(거짓)의 값에 대해 논리 동작을 상태로
semicircuit.tistory.com
※1. 카르노맵
- AND와 OR 게이트로 이루어진 부울함수를 맵에 배치하고 사각형을 조합하여 부울 식을 간략화 할 수 있게 해주는 방법이다.
▶1. 카르노맵 규칙의 종류
-Minterm(Sum Of Product) : 1을 기준으로 셀을 묶는다. 셀끼리 곱하고 묶은 그룹끼리는 곱하여 논리 식을 구성한다.
( 1로 묶일 경우 원래의 변수로 0으로 묶일 경우 원래의 변수에 바를 붙여 표현)
-Maxterm(Product Of Sum) : 0을 기준으로 셀을 묶는다. 셀끼리는 더하고 묶은 그룹끼리는 더하여 논 리식을 구성한다.
( 1로 묶일 경우 변수에 바를 붙이고 0으로 묶일 경우 원래의 변수로 표현)
=> 일반적으로 Minterm 방식으로 카르노맵을 구성한다.
▶2. 카르노맵 사용 방법(과정)
(1) 논리식의 변수를 column과 row에 나눠서 배치한다.
(2) 변수의 신호의 모든 경우를 첫 번째 column과 row에 기입한다. 구체적인 필수적인 규칙은 없으나 인접한 셀 간에 한 변수만 바뀌도록 배치하는 것(Gray코드의 형태: 1비트씩만 변화)이 효율적이다.
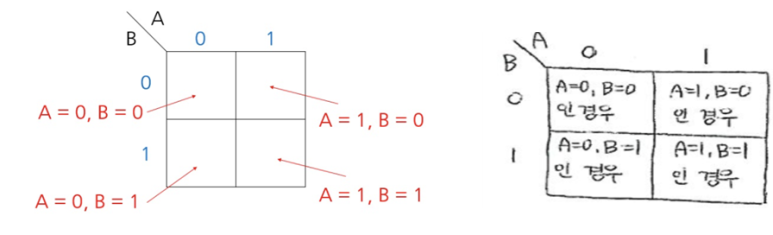
(3) 셀들에는은 각 Column의 변수와 Row의 변수의 교집합 부분에 신호를 입력한다.
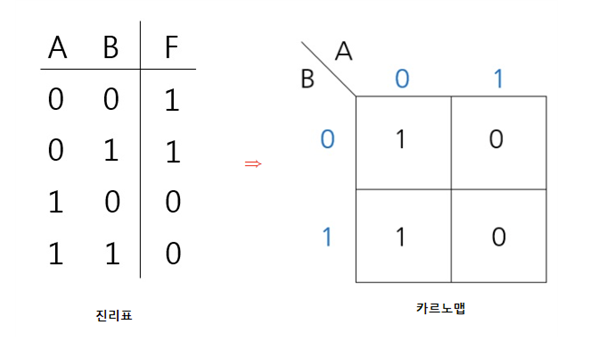
(4) 카르노맵의 그룹화
<카르노맵의 그룹화 규칙>
* 정사각형, 직사각형의 형태로만 묶을 수 있다.
* 이웃하는 셀을 2의 지수의 승(1 ,2, 4....)개씩 묶는다. * 가능한 많은 셀을 포함하는 그룹으로 묶는 것이 더욱 효율이 좋은 간략화를 할 수 있다.
* 네 변에 있는 셀들을 서로 반대편에 있는 셀들과 이웃해 있는 것으로 묶을 수 있다.
* 묶은 공간을 중복할 수 있다.
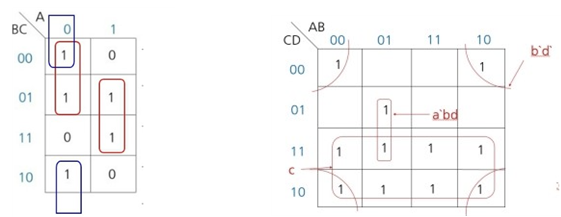
(5) 논리 식으로 표현
➀ Minterm(sum of product)의 경우 1은 기준으로 묶은 셀끼리 곱하고 그룹끼리 더하여 논리 식을 구성 한다.
➁ Maxterm(Product of Sum)의 경우 0을 기준으로 묶은 셀끼리 더하고 그룹끼리 곱하여 논리식을 구성 한다.
<셀의 개수에 따른 그룹에서 논리 게이트 개수 -4변수 카르노맵의 경우>
- 그룹내의 셀의 개수가 1개 : Minterm=> 4개의 And gate / Maxterm=> 4개의 OR gate
- 그룹내의 셀의 개수가 2개 : Minterm=> 3개의 And gate / Maxterm=> 3개의 OR gate
- 그룹내의 셀의 개수가 4개 :Minterm=> 2개의 And gate / Maxterm=> 2개의 OR gate
- 그룹내의 셀의 개수가 8개 :Minterm=> 1개의 And gate / Maxterm=> 1개의 OR gate
- 그룹내의 셀의 개수가 16개 : 0개의 Gate
(6) 결과
=> 간략화된 식을 추출하는데, 같은 결과를 줌으로써 회로를 설계하는데 소자의 개수, 입력의 개수 등을 줄여 주어 보다 효율적인 회로 설계를 하는데 도움을 준다.
▶3. Don't Care(무정의)
- 출력이 정의되지 않는 부분의 경우
- 카르노맵의 각 셀 값이 이든 1이든 관계없이 같은 부울 함수의 값을 갖는다.
- 일반적으로 카르노맵에서 x로 표현한다.
- 가능한 큰 규모의 그룹화를 위해 효율적으로 사용해야한다.
- 숫자의 표현 방식에 따라 진리표와 논리식이 차이가 있을 수
있다. ex) 9에서 d부를 on해도 off해도 9의 형상이 나온다.
▶4. Seven Segment의 카르노맵의 이용
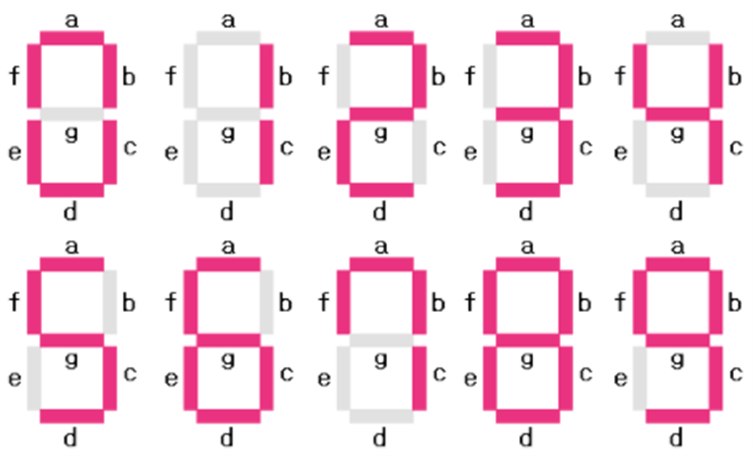
(1) Seven Segment의 종류
➀ COMMON ANODE : 0의 신호에 Segment ON
➁ COMMON CATHODE : 1의 신호에 Sement ON
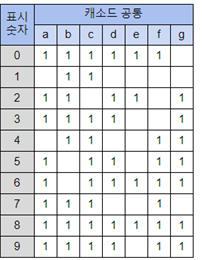
(2) Seven Segment의 표현
(3) 진리표의 표현( COMMON CATHOD )
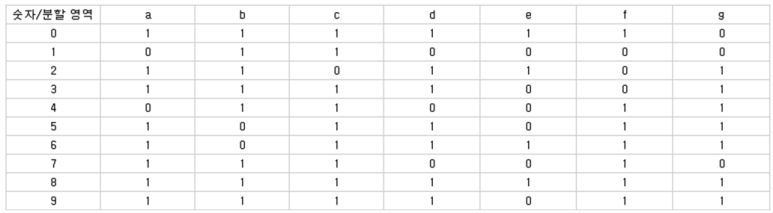
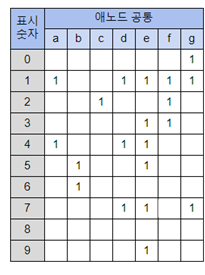
(4) 각 a~g까지의 Minterm식 카르노맵 (COMMON CATHOD)
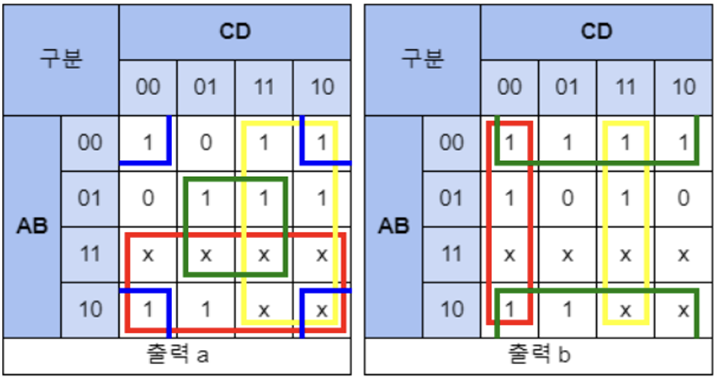
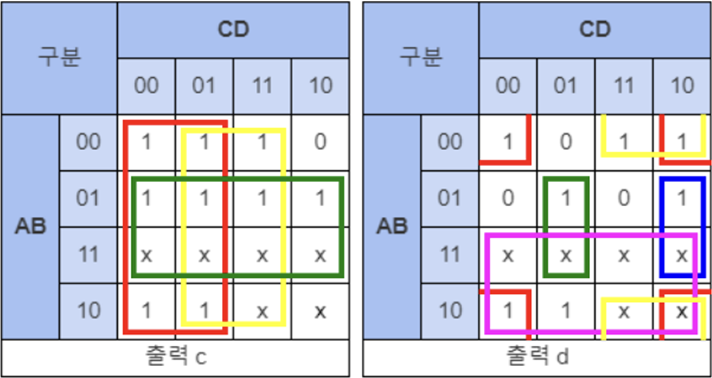
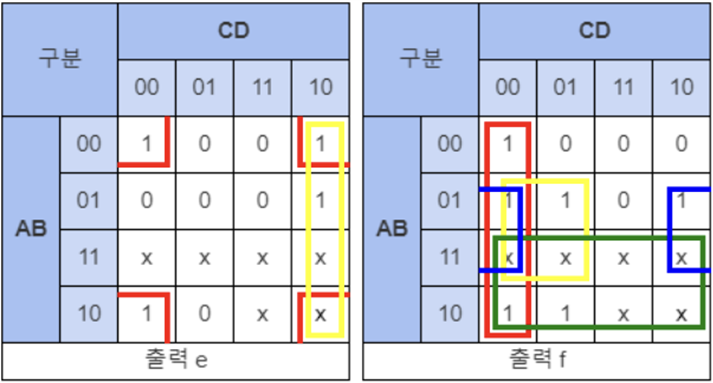
(5) 회로 설계
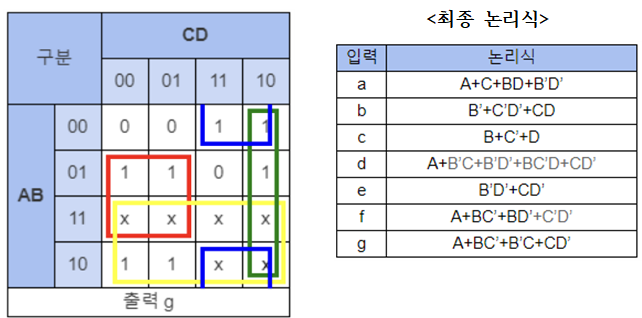
=> 다음 과정을 통해 간략화된 회로를 설계할 수 있다.
▶5. 브레드 보드를 이용한 회로 설계
- 브레드 보드는 전자회로의 시제품을 만드는데 사용하는 재사용할 수 있는 무떔납 장치이다. 이것은 만능 기판에서의 회로 설계처럼 하나하나 납떔 하는 번거러움을 없애주고 재사용이 가능하다.
-이러한 브레드 보드를 이용하여 회로를 직접 설계하고 구현해 보는 과정을 할 수 있다 간단한 게이트의 사용부터 7-Sigment를 지나 응용된 회로 설계가 가능하다.

(1) AND게이트를 다음과 같이 브래드 보드를 통해 설계가능하다.


(2) 아래의 진리표를 카르노 맵으로 간략화 한 것을 설계해 볼 수 있다.
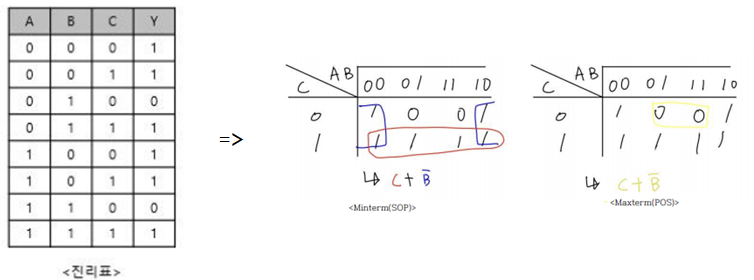

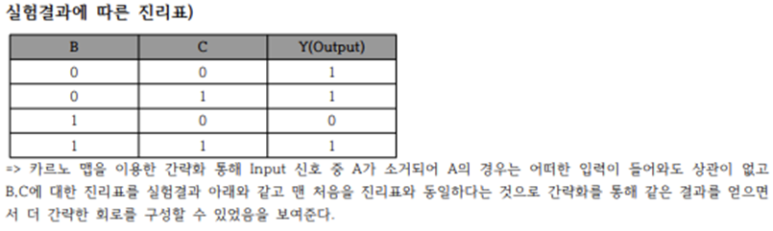
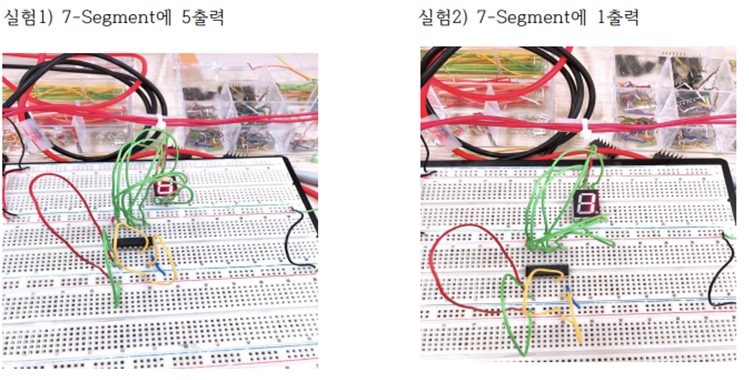
(3) 7-Segment를 7- Segment Driver IC(74LS47)를 이용하여 BCD코드로 변환하고 BCD 코드 출력을 7 Segment를 이용하여 확인해볼 수 있다.
참고) BCD코드 : 2진화 10진수 가중치 코드로 디지털 시계와 같이 10진수를 표시하는데 사용 하는 코드이다.
(4) 여러개의 입력과 IC를 사용하여 새로운 형태의 기능을 하는 프로그램(시스템)을 설계할 수 있다.
ex 비교기 : 입력되는 2개의 값을 비교하여 같으면 해당 수를 다르면 0을 출력하는 회로) -다음은 7-Segment Common Anode Type로 설계된 것으로 7-Segment에 0의 신호가 전달될 때 불이 켜지는 구조이다.
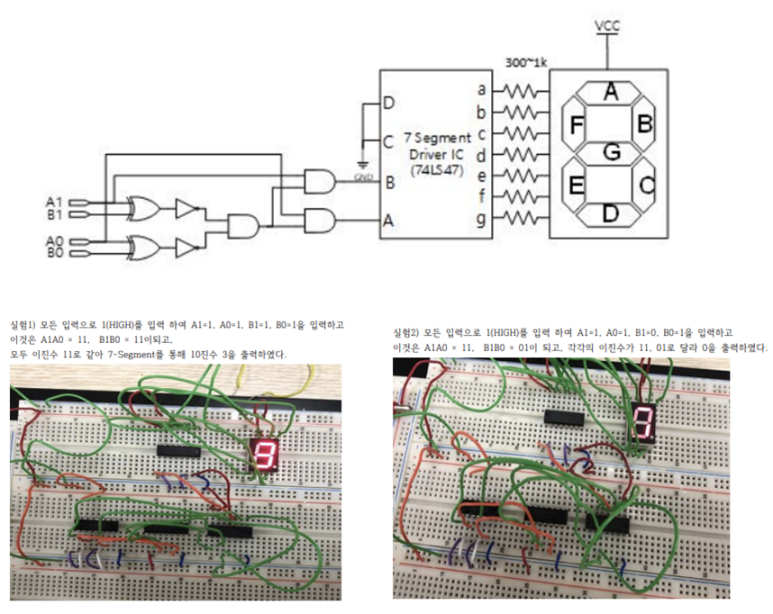
=> Quartus Tool과 같은 논리 시뮬레이션이 가능한 Tool을 통하여 가상 시뮬레이션을 통해 가상의 회로를 구현해 볼 수도 있지만 Bread Board를 통해 비교적 쉽게 회로를 직접 구현해 볼 수 있고 불이 직접 켜지고 시스템이 작동하는 것을 보기 위해 효과적이다.
=> 조합과 회로 설계의 방향에 따라 무한한 종류의 기능의 회로를 설계 할 수 있다.

'University curriculum > [Course] Digital Engineering' 카테고리의 다른 글
| [디지털 공학(12)] NAND와 NOR 게이트의 범용성 (0) | 2024.05.09 |
|---|---|
| [디지털 공학(11)] 논리회로의 해석(조합논리회로, 순서논리회로) (0) | 2024.05.09 |
| [디지털 공학(9)] 부울 대수와 논리 간략화 (0) | 2024.05.09 |
| [디지털 공학(8)] 고정 및 프로그래밍 가능 논리, 전파 지연 시간(Propagation Delay), 팬 아웃 (0) | 2024.05.08 |
| [디지털 공학(7)] 논리 게이트의 이해 (1) | 2024.05.08 |

전자공학 블로그에 오신 것을 환영합니다! 최신 기술 동향, 회로 설계, 반도체 및 전자 부품에 대한 유용한 정보와 실습 팁을 제공합니다.
![[디지털 공학(12)] NAND와 NOR 게이트의 범용성](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FI3fqk%2FbtsHdevnEqy%2Fdo6t1Do74Su1et1bjaqS5k%2Fimg.png)
![[디지털 공학(11)] 논리회로의 해석(조합논리회로, 순서논리회로)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fqf5UK%2FbtsHdvYdnDm%2FUacqQSQ2Q8WbIL4X8jVms0%2Fimg.png)
![[디지털 공학(9)] 부울 대수와 논리 간략화](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FNqlhr%2FbtsHd9N6PWF%2FczmKpK9UYIXpA5wqx47G5k%2Fimg.png)
![[디지털 공학(8)] 고정 및 프로그래밍 가능 논리, 전파 지연 시간(Propagation Delay), 팬 아웃](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fbb6swO%2FbtsHcUDU9wC%2FaKkUfPkPSYIxRVBBMIlkKk%2Fimg.png)