![[디지털 공학(11)] 논리회로의 해석(조합논리회로, 순서논리회로)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fqf5UK%2FbtsHdvYdnDm%2FUacqQSQ2Q8WbIL4X8jVms0%2Fimg.png)

안녕하세요.
이번 시간에는 조합 논리회로와 순서 논리회로를 비교하고 드모르간 또는 불 대수 연산으로부터 대치(동일하다고 표현) 가능한 논리연산에 대해 작성하겠습니다.
※1. 논리회로의 해석
▶1. 조합 논리회로와 순서 논리회로
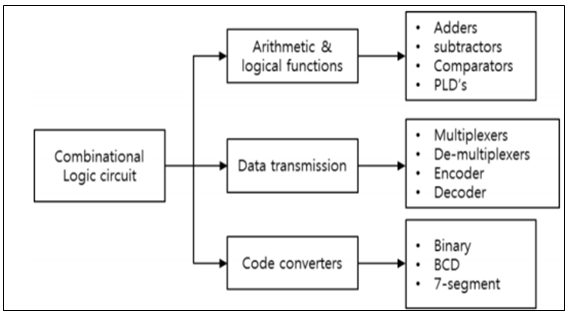
(1) 조합 논리회로
<특징>
⓵ 입력의 조합에 의해서만 출력이 결정된다.
⓶ 저장 & 기억이 불가능하다.
ex) 반가산기, 전가산기, 병렬가산기, 감산기, 디코더, 인코더, 멀티플렉서, 연산기, 디멀티프렉서, 비교기 등
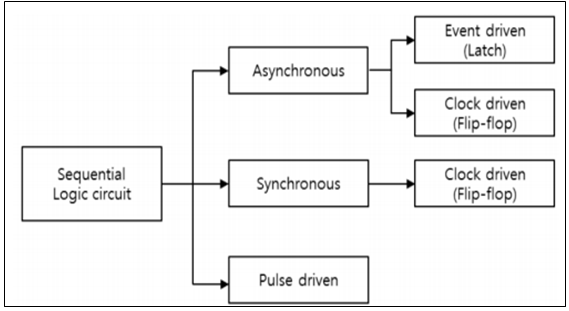
▶2. 순서 논리회로
<특징>
⓵ 입력과 내부 상태의 조합에 의해 출력이 결정된다.
⓶ 저장 & 기억이 가능하다.
ex) 플립플롭, 카운터, 레지스터, ROM, PLA, 플래쉬 메모리 등
※2. 기본적인 조합 논리 회로
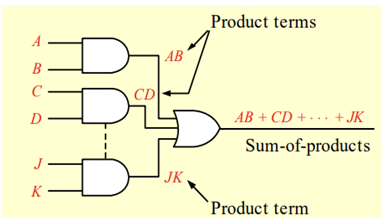
▶1. AND-OR 논리
- 곱의 합(SOP)식은 AND-OR 게이트를 조합하여 기본적인 논리회로로 구현된다.
▶2. AND-OR-Inverter 논리
- 곱의 합(SOP) 출력이 반전된 경우, AND-OR-Invert 회로라고 한다.
-AND-OR-Invert(AOI)는 드모르간 법칙과 불 대수를 이용하여 SOP에서 POS로 바꿀 수 있다.(두 번의 드모르간 법칙) => AO와 AOI의 대치
ex) ((AB)+(CD))'=(A'+B')(C'+D')
(ABC'+D'E)'=(A'+B'+C)(D+E')
⓵
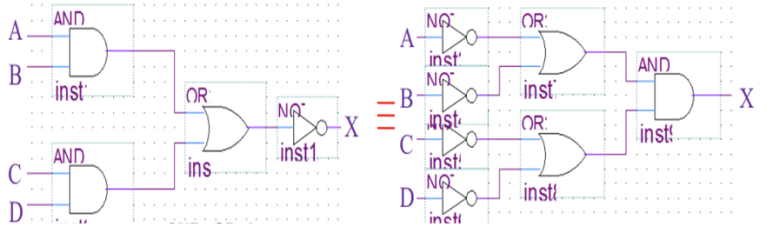
⓶
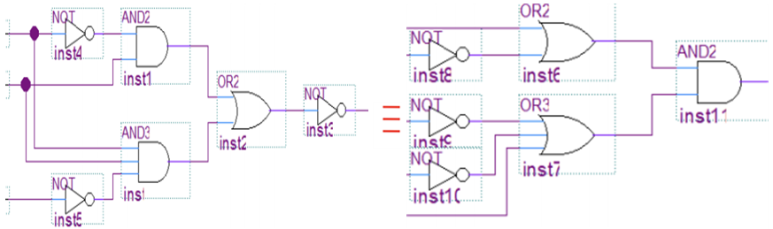
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
cf) OR <-> AND 대치
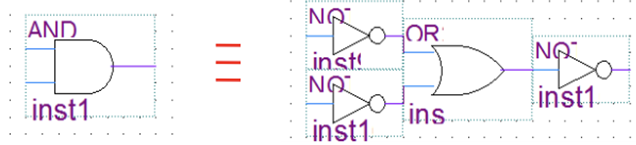
- 각각의 입력과 출력에 NOT(부정)을 취하면 등가로 대치할 수 있다.
즉, AND의 입력과 출력에 NOT(입력이 2개일때 총 NOT 3개) 붙이면 오리지널한 OR과 같은 출력을 내는 회로이다.
또는, OR의 입력과 출력에 NOT(입력이 2개일 때 총 NOR 3개) 붙이면 오리지널한 AND와 같은 출력을 내는 회로이다.
(1) AND = (NOT+NOT)+OR+(NOT)
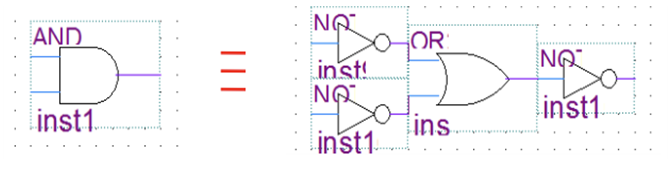
(2) OR = (NOT+NOT)+AND+(NOT)
응용)
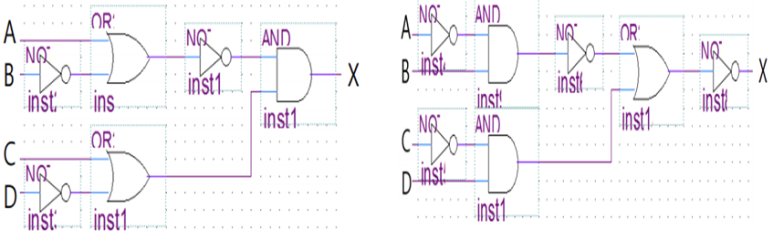
=> 두 개는 AND <-> OR 대치를 통해 만들 회로로 같은 출력을 가진다.
두 게이트 사이에는 경우 입력의 NOT과 출력의 NOT에 의해 이중 부정으로 변화가 없다.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------

'University curriculum > [Course] Digital Engineering' 카테고리의 다른 글
| [디지털 공학(13)] 조합논리의 기능(반가산기, 전가산기 설계 // 덧셈기, 덧뺄셈기) _ 조합논리회로 (1) (0) | 2024.05.09 |
|---|---|
| [디지털 공학(12)] NAND와 NOR 게이트의 범용성 (0) | 2024.05.09 |
| [디지털 공학(10)] 카르노맵 (0) | 2024.05.09 |
| [디지털 공학(9)] 부울 대수와 논리 간략화 (0) | 2024.05.09 |
| [디지털 공학(8)] 고정 및 프로그래밍 가능 논리, 전파 지연 시간(Propagation Delay), 팬 아웃 (0) | 2024.05.08 |

전자공학 블로그에 오신 것을 환영합니다! 최신 기술 동향, 회로 설계, 반도체 및 전자 부품에 대한 유용한 정보와 실습 팁을 제공합니다.
![[디지털 공학(13)] 조합논리의 기능(반가산기, 전가산기 설계 // 덧셈기, 덧뺄셈기) _ 조합논리회로 (1)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbupB76%2FbtsHed35Ljo%2F7LXgMKrS3XCp4v2kCNJRT1%2Fimg.png)
![[디지털 공학(12)] NAND와 NOR 게이트의 범용성](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FI3fqk%2FbtsHdevnEqy%2Fdo6t1Do74Su1et1bjaqS5k%2Fimg.png)
![[디지털 공학(10)] 카르노맵](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FOAoIQ%2FbtsHbQvxeYU%2FHD8b1aV0WcT7lbeeH9enJk%2Fimg.png)
![[디지털 공학(9)] 부울 대수와 논리 간략화](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FNqlhr%2FbtsHd9N6PWF%2FczmKpK9UYIXpA5wqx47G5k%2Fimg.png)